本文讲解了如何通过斜率来理解和重建曲线。首先从恒定斜率的直线入手,说明直线的位置取决于一个未定常数。接着讨论斜率随 x 值变化的复杂情况,展示了通过累加小段近似重建曲线的方法。最后指出,积分可以通过累加无限小的变化精确重建曲线,并且需要一个未定常数来表示曲线的初始高度。
第 17 章 积分
此前我们已经揭示了一个伟大的秘密,那就是这个神秘的符号 $\int$,实际上只是一个拉长了的 $S$,仅仅意味着“总和”或者“所有此类量的总和”。因此,它类似于另一个符号 $\sum$ (希腊字母 Sigma),也是一个求和的标志。然而,在数学家的实践中,这些符号的使用有一些不同之处:$\sum$ 通常用来表示有限多个量的总和,而积分符号 $ \int$ 则通常用来表示对无数个无限小的微小量的总和,这些微量共同组成了所需的总量。例如,$\int dy = y$,$\int dx = x$。
任何人都能理解,整体都可以被想象为由许多小部分组成;而这些部分越小,它们的数量就会越多。例如,一条一厘米长的线可以被想象成由 $10$ 段组成,每段 $\frac{1}{10}$ 厘米长;或者由 $100$ 段组成,每段 $\frac{1}{100}$ 厘米长;或者由 $1,000,000$ 段组成,每段 $\frac{1}{1,000,000}$ 厘米长;再或者,将这一思想推至极限,它可以被视为由无数个无限小的部分组成。
你可能会说,这种方式有什么意义呢?为什么不直接将整体看作整体?答案很简单:在许多情况下,我们无法直接计算出整体的大小,必须通过加总许多小部分来实现。“积分”的过程正是为了让我们能够计算出那些无法直接估计的总量。
我们先从一两个简单的例子入手,以熟悉这一加总许多部分的概念。
考虑以下级数:
\[ 1 + \tfrac{1}{2} + \tfrac{1}{4} + \tfrac{1}{8} + \tfrac{1}{16} + \tfrac{1}{32} + \tfrac{1}{64} + \ldots \]
在这个级数中,每一项的值都是前一项的一半。如果我们可以无限延续下去,这个总和的值是多少?每个学生都知道答案是 $2$。可以这样想:将其看作一条线。开始时是一厘米;加上半厘米,再加上四分之一厘米,再加上八分之一厘米,依此类推。如果在某个步骤停止,还会有一部分尚未加上以组成完整的 $2$ 厘米;而这未加上的部分总是与最后一次加上的部分一样大。例如,如果在加上 $1$、$\frac{1}{2}$ 和 $\frac{1}{4}$ 后停止,还会有 $\frac{1}{4}$ 未加上。如果我们继续到加上 $\frac{1}{64}$,仍然会有 $\frac{1}{64}$ 未加上。这个剩余部分总是等于最后一项的大小。只有通过无穷次操作,才能真正达到 $2$ 厘米的总和。实际上,当我们加到那些小到无法画出的部分时就可以认为达到了总和——这大约需要10项,因为第11项是 $\frac{1}{1024}$。如果我们想要小到连最精密的测量仪都无法检测,那只需大约20项即可。即便是显微镜,也无法显示出第18项!因此,无穷次操作实际上并没有那么可怕。积分就是这样一个完整的总和。然而,正如我们将看到的,在某些情况下,积分运算能让我们精确计算出通过无穷次操作得到的总量。在这些情况下,积分运算提供了一种快速且简便的方法,来得到一个原本需要无穷复杂步骤才能得出的结果。所以我们最好立刻开始学习“如何积分”。

曲线的斜率与曲线本身
我们先做一些关于曲线斜率的初步探讨。我们已经知道,求曲线的导数意味着找到其斜率(或在不同点上的斜率)的表达式。那么,如果定了斜率(或斜率的表达式),是否可以进行反向操作,从而重建整个曲线呢?
回到这里的情况 (2)。我们考虑最简单的曲线——一条斜直线,其方程为:
\[ y = ax+b. \]

在这里,$b$ 表示当 $x=0$ 时 $y$ 的初始高度,而 $a$(即 $\dfrac{dy}{dx}$)表示这条直线的“斜率”。这条直线的斜率是恒定的。在直线的每一部分上,基本的三角形

的高与底始终保持相同比例。假设我们将 $dx$ 和 $dy$ 取为有限量,例如 $10$ 个 $dx$ 构成一厘米,那么会有 $10$ 个小三角形,如下所示:

现在,假设我们要从 $\dfrac{dy}{dx} = a$ 这个信息开始,重建这条“曲线”。该怎么做呢?依然取这些小 $d$ 为有限大小,我们可以画出 $10$ 个这样的 $d$,所有的斜率都相同,然后将它们首尾相连,如下图所示:

由于斜率对于所有部分都是相同的,这些小 $d$ 将连接成一条如图 48所示的斜直线,其斜率为 $\dfrac{dy}{dx} = a$。只要我们认同 $y$ 是所有 $dy$ 的总和,$x$ 是所有 $dx$ 的总和,无论取 $dy$ 和 $dx$ 为有限还是无限小(它们始终相同),显然有 $\dfrac{y}{x} = a$,然而,我们应该把这条斜线放在哪里?是从原点 $O$ 开始,还是从更高处开始?由于只有关于斜率的信息,因此无法确定其具体的初始高度。无论初始高度如何,斜率始终相同。因此,我们可以假设一个合理的高度,从 $O$ 点上方 $C$ 的位置开始。这时,我们得到的方程是:
\[ y = ax + C. \]
在这种情况下,添加的常数显然表示当 $x=0$ 时 $y$ 的具体值。
接下来,我们看一个更复杂的例子,即一条斜率不是恒定的曲线,而是斜率逐渐增加的曲线。假设上升的斜率随着 $x$ 的增长而逐渐变大。用符号表示为:
\[ \frac{dy}{dx} = ax. \]
具体情况下,取 $a = \frac{1}{5}$,因此:
\[ \frac{dy}{dx} = \tfrac{1}{5} x. \]
我们最好先计算一些不同 $x$ 值下的斜率值,并画出它们的小图。
| $x =0$ | $ \frac{dy}{dx} = 0, $ |  |
|---|---|---|
| $x =1$ | $ \frac{dy}{dx} = 0.2, $ |  |
| $x =2$ | $ \frac{dy}{dx} = 0.4, $ | 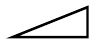 |
| $x =3$ | $ \frac{dy}{dx} = 0.6, $ | 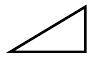 |
| $x =4$ | $ \frac{dy}{dx} = 0.8, $ | 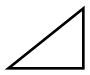 |
| $x =5$ | $ \frac{dy}{dx} = 1.0. $ | 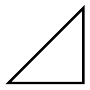 |
接着尝试将这些小片段拼接起来,使每个片段的底部中点位于正确的水平位置,并在角点处彼此吻合,如图49。结果当然不会是一条平滑的曲线,而是一个对曲线的近似。如果我们将片段减小为原来的一半,但数量加倍,如图50,会得到一个更好的近似。然而,要得到一条完美的曲线,我们应该将每个 $dx$ 和其对应的 $dy$ 取得无限小且数量无限多。


那么,在任何点 $P$ 上,$y$ 的值应该是多少呢?显然,在曲线上的任意点 $P$,$y$ 的值是从 $0$ 到该点的所有小 $dy$ 的总和,即 $\int dy = y$。由于每个 $dy$ 都等于 $\frac{1}{5}x · dx$,因此整个 $y$ 就是所有 $\frac{1}{5}x · dx$ 的总和,用积分表示为 $\int \tfrac{1}{5}x · dx$。
如果 $x$ 是一个常数,那么 $\int \tfrac{1}{5}x · dx$ 等于 $\frac{1}{5} x \int dx$,即 $\frac{1}{5}x^2$。但 $x$ 是从 $0$ 开始,增长到点 $P$ 的特定值,因此它从 $0$ 到该点的平均值是 $\frac{1}{2}x$。因此,$\int \tfrac{1}{5} x\, dx = \tfrac{1}{10} x^2$,或 $y=\frac{1}{10}x^2$。
但与之前的情况一样,这需要添加一个未定常数 $C$,因为我们不知道曲线在 $x=0$ 时从原点上方的哪个高度开始。因此,画在图51中的曲线方程为:
\[ y = \tfrac{1}{10}x^2 + C. \]

