在整个微积分中,我们处理的是不断增长的量以及增长的速率。我们将所有的量分为两类:常量和变量。那些我们认为是固定值的量,称为常量,通常用字母 \(a\)、\(b\) 或 \(c\) 等字母表示;而那些认为可以增长(或者像数学家所说的“变化”)的量,用字母 \(x\)、\(y\)、\(z\)、\(u\)、\(v\)、\(w\),或有时用 \(t\) 来表示。
此外,我们通常同时处理多个变量,考虑一个变量如何依赖于另一个变量。例如,我们思考投射物到达的高度如何取决于到达该高度所用的时间。或者考虑一个给定面积的矩形,其长度增加时,宽度会如何相应地减少。又或者思考梯子的倾斜角度发生变化时,梯子到达的高度会如何变化。
假设我们有两个这样的变量,它们之间有相互依赖的关系。一个变量的改变会导致另一个变量的改变,因为它们之间存在这种依赖关系。设其中一个变量为 \(x\),另一个依赖于它的变量为 \(y\)。
假设我们让 \(x\) 变化,也就是说,让它增加一点,记为 \(dx\)。这样 \(x\) 就变成了 \(x + dx\)。因为 \(x\) 发生了变化,\(y\) 也会随之变化,变成 \(y + dy\)。在这里,\(dy\) 的值可能为正,也可能为负;而且它的大小通常不会(除非极其偶然)等于 \(dx\) 的大小。
举两个例子。
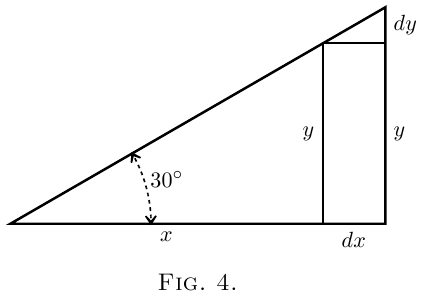
(1)令 \(x\) 和 \(y\) 分别为直角三角形(图4)的底边和高,而斜边的倾斜角度固定为 \(30°\)。我们假设这个三角形在扩展的同时保持最初的角度不变,那么当底边增长为 \(x + dx\) 时,高度会变为 \(y + dy\)。在这里,增加 \(x\) 会导致 \(y\) 的增加。小三角形的高为 \(dy\),底边为 \(dx\),它与原三角形相似;显然,\(\dfrac{dy}{dx}\) 的比率与 \(\dfrac{y}{x}\) 的比率相同。由于角度是 \(30°\),我们可以看到这里
(2)在图5中,设 \(x\) 表示梯子底端距墙的水平距离 \(AB\),梯子长度固定,而 \(y\) 表示其在墙上到达的高度。现在显然 \(y\) 依赖于 \(x\)。很容易看出,如果将底端 \(A\) 稍微移开一点,顶端 \(B\) 会稍微降低。用科学语言描述这一情况:如果我们将 \(x\) 增加为 \(x + dx\),那么 \(y\) 将变为 \(y - dy\);即当 \(x\) 获得正增量时,\(y\) 的增量是负的。
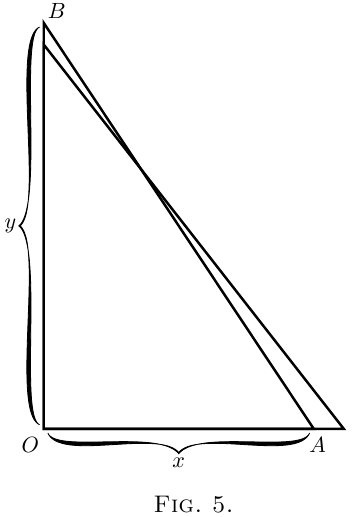
那么具体是多少呢?假设梯子足够长,使得当底端 \(A\) 离墙 \(19\) 厘米时,顶端 \(B\) 刚好离地 \(1.8\) 米。如果将底端拉出 \(1\) 厘米,顶端会下降多少?全部换算成厘米:\(x = 19\) 厘米,\(y = 180\) 厘米。增量 \(dx\) 为 \(1\) 厘米,即 \(x + dx = 20\) 厘米。
\(y\) 减少的量是多少?新高度将为 \(y - dy\)。用勾股定理可以算出 \(dy\) 的大小。梯子的长度为
显然,新高度 \(y - dy\) 将满足以下条件:
现在 \(y\) 为 \(180\),所以 \(dy = 180 - 179.89 = 0.11\) 厘米。
因此,我们看到使 \(dx\) 增加 \(1\) 厘米导致 \(dy\) 减少 \(0.11\) 厘米。
而 \(dy\) 对 \(dx\) 的比率可以表示如下:
也可以看出,除了一种特殊位置外,\(dy\) 的大小一般不会与 \(dx\) 相同。
在整个微分计算中,我们一直在寻找一个有趣的量,实际上是一个比率,即当它们都无限小的时候,\(dy\) 与 \(dx\) 的比例。
需要注意的是,只有当 \(y\) 和 \(x\) 之间存在某种关系时,才能找到这个比率 \(\dfrac{dy}{dx}\),因此当 \(x\) 变化时 \(y\) 也会随之变化。例如,在第一个例子中,当三角形的底边 \(x\) 变长时,其高度 \(y\) 也会增加;而在第二个例子中,当梯子的底端与墙的距离 \(x\) 增加时,梯子所到达的高度 \(y\) 则相应减少,起初减少较慢,但随着 \(x\) 增大,减少得越来越快。在这些情况下,\(x\) 与 \(y\) 之间的关系完全明确,可以用数学表达出来,例如 \(\dfrac{y}{x} = \tan 30°\) 和 \(x^2 + y^2 = l^2\)(其中 \(l\) 是梯子的长度),并且 \(\dfrac{dy}{dx}\) 有我们在每个例子中找到的意义。
如果 \(x\) 仍表示梯子底端到墙的距离,而 \(y\) 则表示墙的水平长度,或墙中的砖数,或自墙建成以来的年数,任何对 \(x\) 的改变都不会对 \(y\) 产生任何影响;在这种情况下 \(\dfrac{dy}{dx}\) 没有任何意义,也无法找到其表达式。当我们使用微分 \(dx\)、\(dy\)、\(dz\) 等时,\(x\)、\(y\)、\(z\) 等之间必须存在某种关系,这种关系称为 \(x\)、\(y\)、\(z\) 的“函数”;例如上述表达式 \(\dfrac{y}{x} = \tan 30°\) 和 \(x^2 + y^2 = l^2\) 就是 \(x\) 和 \(y\) 的函数。这些表达式隐含地(即没有明确显示)包含了将 \(y\) 表示为 \(x\) 的函数,或将 \(x\) 表示为 \(y\) 的函数,因此它们被称为 \(x\) 和 \(y\) 的隐函数;可以分别写成
和
这些最后的表达式明确地(即清晰地)表示出 \(y\) 关于 \(x\) 或 \(x\) 关于 \(y\) 的值,因此被称为 \(x\) 或 \(y\) 的显函数。例如 \(x^2 + 3 = 2y - 7\) 是 \(x\) 和 \(y\) 的隐函数;可以写成 \(y = \dfrac{x^2 + 10}{2}\)(\(x\) 的显函数)或 \(x = \sqrt{2y - 10}\)(\(y\) 的显函数)。我们可以看到 \(x\)、\(y\)、\(z\) 等的显函数是一个随 \(x\)、\(y\)、\(z\) 等变化而变化的值,可以是一个变量或多个变量一起变化。因此,显函数的值称为因变量,因为它依赖于函数中其他变量的值;这些其他变量称为自变量,因为它们的值不依赖于函数所取的值。例如,如果 \(u = x^2 \sin \theta\),\(x\) 和 \(\theta\) 是自变量,而 \(u\) 是因变量。
有时几个量 \(x\)、\(y\)、\(z\) 之间的确切关系未知,或者不方便陈述;仅知道或方便陈述的是这些变量之间存在某种关系,使得 \(x\)、\(y\)、\(z\) 等量不能单独变化而不影响其他量;此时函数关系可用 \(F(x, y, z)\) 表示(隐函数),或用 \(x = F(y, z)\),\(y = F(x, z)\) 或 \(z = F(x, y)\)(显函数)表示。有时字母 \(f\) 或 \(\phi\) 被用来代替 \(F\),因此 \(y = F(x)\)、\(y = f(x)\) 和 \(y = \phi(x)\) 都表示同样的意思,即 \(y\) 的值以某种未说明的方式依赖于 \(x\) 的值。
我们称比率 \(\dfrac{dy}{dx}\) 为“\(y\) 关于 \(x\) 的导数”。这是一个严肃的科学术语,用来描述这个非常简单的概念。但我们不应被严肃的术语吓倒,因为概念本身并不难。与其被吓倒,不如简单地对这种不必要的复杂命名方式表示一下不满,然后继续讨论这个简单的内容,即比率 \(\dfrac{dy}{dx}\)。
在学校学过的普通代数中,你总是在寻找一些被称为 \(x\) 或 \(y\) 的未知数;有时还需要同时找到两个未知数。而现在,你需要以一种新的方式去“寻找”,目标不再是 \(x\) 或 \(y\) 本身,而是这个被称为 \(\dfrac{dy}{dx}\) 的奇特比率。求 \(\dfrac{dy}{dx}\) 的过程称为“求导”。但是,请记住,我们想要的是在 \(dy\) 和 \(dx\) 都无限小的情况下,这个比率的值。导数的真实值是当它们被视为极微小的时候所接近的极限。
现在让我们学习如何去寻找 \(\dfrac{dy}{dx}\)。
第3章注 如何读微分符号
不要犯初学者的错误,认为 \(dx\) 意味着 \(d\) 乘以 \(x\),因为 \(d\) 并不是一个因子,它表示变量的微小变化。\(dx\) 应读作“dee-eks”。
如果读者没有人指导这方面的内容,这里简单说明一下如何读这些导数。\(\dfrac{dy}{dx}\) 读作 y 关于 x 的导数。同样,\(\dfrac{du}{dt}\) 表示 u 关于 t 的导数。
二阶导数将在后面遇到。它们像这样: \(\dfrac{d^2 y}{dx^2}\),表示 y 关于 x 的二阶导数,意思是对 \(y\) 关于 \(x\) 的求导运算已经(或必须)进行两次。
另一种表示函数已经被求导的方式是给函数符号加上一个撇号。因此,如果 \(y=F(x)\) 表示 \(y\) 是 \(x\) 的某个未具体说明的函数,我们可以写成 \(F'(x)\) 来代替 \(\dfrac{d\bigl(F(x)\bigr)}{dx}\)。类似地,\(F''(x)\) 表示原函数 \(F(x)\) 已对 \(x\) 求导了两次。
